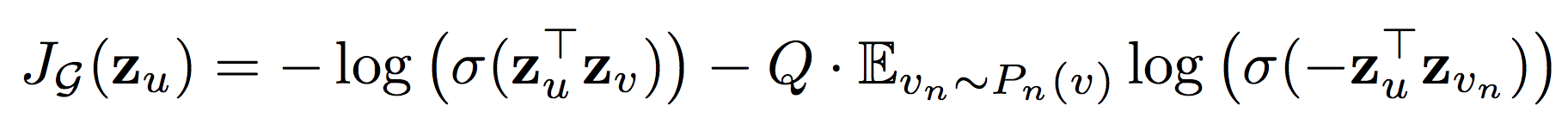[NOTES] Inductive Representation Learning on Large Graphs

ArXiv (NIPS ‘17)

What?

GraphSAGE (SAmple and aggreGatE): A general inductive learning framework for node embeddings.

Why?

Most recent work (e.g. ¹) has focus on the transductive setting, in which the graph is fixed so the goal is to predict label information for unlabelled (not unseen) nodes. If a new node was to be added, the entire embedding would need to be recomputed, making the methods costly for dynamic or dense graphs, as well as making it difficult to train in a mini-batch setting.

How?

Instead of learning individual embeddings for each node, GraphSAGE learns functions that generate the embeddings for a node, which sample and aggregate feature
and topological information from the node’s neighbourhood.

Figure 1: The GraphSAGE algorithm ²

The weights for composing neighbouring embeddings and the parameters of the aggregation function are learned with a usual embedding loss, which pushes nearby nodes to have similar representations in the embedding space and separates distinct nodes. Note that the embedding $\mathbf{z}_u$ is generated from neighborhood information rather than training a unique embedding for each node.

Figure 2: Loss ²

The authors propose and compare three aggregator candidates. These must be symmetric: a permutation of the inputs should not change the result, since the “ordering” of a graph is arbitrary.

• Mean Aggregator: close to GCN ¹ as a linear approximation of a localized spectral convolution
• LSTM Aggregator: Larger expressive power but not inherently symmetric
• Pooling Aggregator: No significant difference between max- and mean-pooling.

Appendix: Mini-batch setting

Figure 3: GraphSAGE mini-batch setting ²

The required nodes are sampled first, so that the mini-batch “sets” (nodes needed to compute the embedding at depth $k$) are available in the main loop, and everything can be run in parallel.

Evaluation

• Subject classification for academic papers (Web of Science citations)
• Community detection classification on Reddit posts
• Protein function classification across graphs in Protein-Protein Interaction

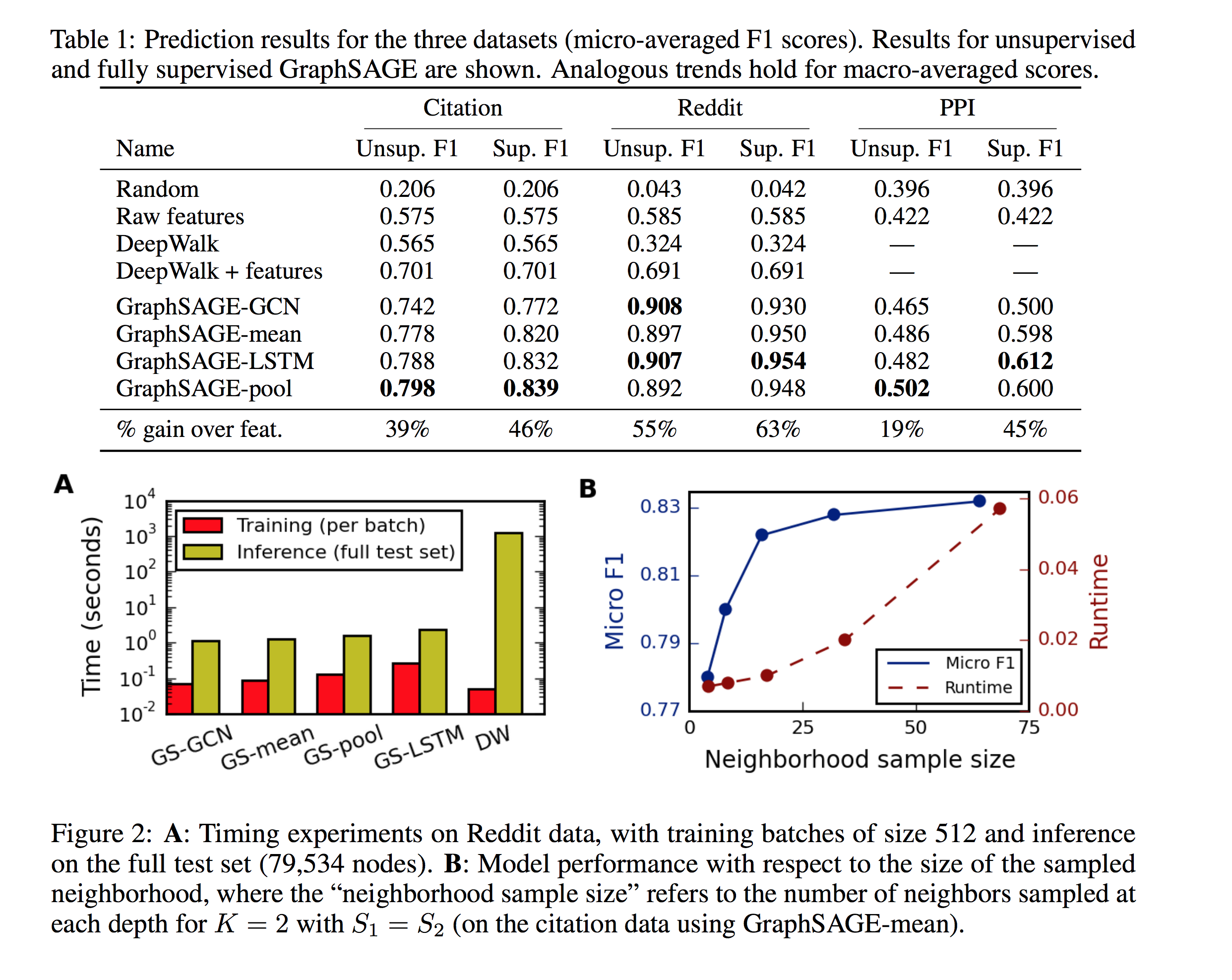
The authors compare against a random classifier, a logistic regression classifier, DeepWalk ³ as an feature learning method, as well as a concatenation of the node features and DeepWalk-generated embeddings. Several variants of GraphSAGE are also compared, with a depth of $K=2$ and respectively $S_1=25$, $S_2=10$ neighbors sampled at depth $k=1,2$.

Comments

• This work uniformly samples a fixed-size set of neighbors instead of using the full neighborhood for computational footprint
• The search depth also appears to show no real improvement after $K=2$
• Different aggregator function for each depth, to compose different information about the neighbours (topological, similarity, …)
• Has the ability to not only generalize to unseen nodes but also to unseen graphs!
• Provides a solution to the mini-batch training problem for graph-based learning (though the sub-sampling and limited depth search also helps the performance gains)
• FastGCN ⁴ has proposed some new sampling methods, and included modern learning techniques to improve results (e.g. dropout, layer normalization, …)

Questions

• How to leverage some priors about the graph structure (e.g. if it follows a powerlaw, Poincaré embeddings ⁵ have been shown to be an efficient embedding)?
• Why is there no improvement for larger depths? Is it akin to the problems faced by deeper feed-forward nets?
• Could this method be used to predict the number of neighbors a given node has? (Theorem 1 seems to indicate that it is possible)
• Several of the graph size parameters are heuristic / hardcoded (depth, neighbor sampling, graph density). Could they be learned / optimized for as hyperparameters?
• Are there mechanisms to prevent re-sampling the same nodes again? (i.e. in a sparse graph the node doesn’t necessarily have $S_k$ neighbors to sample from. Note that the authors specify that this method is designed for large graphs which require subsampling to be treated)
• Could we use non-local operators as aggregator functions? (these non-local operators have shown promising results comparable to local operations like convolutions ^{6 7}) This could require a much smaller neighborhood to capture the same long range dependencies.

Resources

Code

• Tensorflow implementation
• Reference PyTorch implementation

Discussion

• Implementation overview (slides, pdf)
• SNAP lab page
• Jure Leskovec IPAM talk
• Review paper ⁸

References